Time Series Forecasting (2) 파이썬을 이용한 시계열 예측 모델링 - ARIMA (Auto regressive-integrated-moving average), Auto ARIMA
ARIMA 모델은 지나고보니... 가장 traditional하고 오래된만큼 여러 분야의 시계열 연구에 많이 쓰이고, 오래됐음에도 정확도가 나쁘지 않은 편인 것 같다. 공부하는 입장에서 이 모델의 최대 장점은 많이 쓰인만큼 자료가 많다는거다. 땡큐 슨배님들 계속해서 많은 자료를 남겨줘,,, 그럼에도 역시나 한국어 자료는 비교적 적다. 내가 1년에 몇개 안되지만 생각날때마다 개발 포스팅을 남기는 이유!
1. 데이터 계절성 체크하기.
ARIMA 모델을 공부하기 전에 제발 내가 미리 알았더라면 좋았을 건.
이 모델은 가지고 있는 시계열 데이터가 정산성을 보일 때, 즉 데이터가 stationary할 때 최대로 유용하다는 점이다. 이게 무슨 개소리냐고 생각할 수 있다. 그거슨 매우 정상 - stationarity란 계절성을 말하는데, 데이터가 계절에 따라 비슷하거나 다른 점이 있을 때, 계절이 아니더라도 어떤 주기를 가지고 움직일 때 stationary 하지 않다고 한다. 계절성이 없을 때, 즉 주기가 없을 때 stationary하다고 표현한다. 시계열 분석할 때 데이터가 계절성을 띄는지 안띄는지 분석하고 모델링을 해야 헛짓거리를 줄일 수 있다. 그러므로 아직 안했다면 아래 포스팅을 통해 미리 데이터가 Stationary한지 체크하고 오자.
시계열 분석 데이터 Stationarity check - 파이썬으로 데이터의 계절성/주기성 파악하기 (1) ACF, PACF 플
맨땅에 헤딩하듯 시계열예측 모델을 공부하다 보니 알게된 매우 중요한 팁. 예측 모델은 가지고 있는 시계열 데이터의 통계적 특성을 확인하는 것에서 시작해야 한다는 점이다. 현재의 값이 과
happy-chipmunk.tistory.com
2. ARIMA 모델 이해
ARIMA 모델은 AR-I-MA 를 합친 용어다. 아뤼마라니 모델 이름치고 참으로 우아함. LSTM 같은 이름보다 아주 보드랍고 간지럽단 말이징 아무튼 아래 표를 위에서 아래로 차례차례 이해하면 ARIMA가 뭔지 조금이라도 쉽게 알아들을 수 있다. 왼쪽이 모델명이고 오른쪽이 모델에 대한 설명이다.
시계열 데이터가 있다고 치면, 예측하려는 값으로부터 >>
| AR (Auto-regressive) / AR(p) | AR(p) 모델은 p개의 과거 값들을 이용해 예측한다. |
| MA (Moving average) / MA(q) | MA(q) 모델은 q개의 과거 오차 값들을 이용해 예측한다. |
| ARMA(p,q) | ARMA(p,q) 모델은 p개의 과거 값과 q개의 과거 오차 값들을 이용해 예측한다. |
| ARIMA(p,d,q) | 데이터를 d회 차분하고 p개의 과거 값과 q개의 오차 값을 이용하여 예측 그 후 다시 비차분화(차분한 값을 다시 원래의 값으로 변화)하여 예측값 생성 |
즉 ARIMA 모델에서 변수 p,d,q 의 의미는
p: the number of lag observations in the model; also known as the lag order (AR)
--> p개 전 값부터 주르륵 과거 값을 이용함 (p개의 과거 값들을 이용해 예측)
d: the number of times that the raw observations are differenced; also known as the degree of differencing (I)
--> d 만큼 차분함
q: the size of the moving average window; also known as the order of the moving average (MA)
--> q개 전 값부터 주르륵 오차 값을 이용함
예측컨대 아마도 데이터를 d회 차분한다는 부분에서부터 이게 무슨 소리지 했을 것.. 아니면 말고..
differencing은 데이터를 stationary 하게 만들기 위한 과정이다.
a,b,c,d,e,f,...z 라는 시계열테이터가 있다고 치면 1회 차분하면
b-a, c-b, ..., z-y 가 된다. 이 데이터를 가지고 다시 한번 stationarity 를 검사한다. 아직도 계절성이 있으면 다시 한번 차분한다.
데이터가 계절성이 없어지면 그 상태에서 AR과 MA 모델을 돌린 후, 다시 차분한 d횟수 만큼 과거값을 더해주면서 돌아온다.
이 차분 과정을 통해 AR, MA 모델을 계절성없는 데이터로 돌려서 효율을 높이는 것이다.
3. Python으로 ARIMA 모델 돌리기
예시로, 뉴욕시의 2020년 2월 16일부터 2020년 12월 27일까지 매주 일요일 집계된 코로나로 인한 사망률 데이터를 이용해서 마지막 4주간의 사망률을 예측해보겠다.
먼저 필요한 package들을 import 한다.
# 패키지 임포트
import os
import numpy as np
import pandas as pd
from pandas import to_datetime
from matplotlib import pyplot as plt
import seaborn as sns
import itertools
import warnings
import datetime
from datetime import datetime
warnings.filterwarnings('ignore')
%matplotlib inline
# ARIMA 모델 패키지
from statsmodels.tsa.arima_model import ARIMA
from statsmodels.tsa.api import ExponentialSmoothing, SimpleExpSmoothing, Holt
from sklearn.metrics import mean_squared_error
from sklearn.linear_model import LinearRegression
from sklearn import linear_model
# Auto Arima 모델 패키지
# pip install --user pmdarima
import pmdarima as pm
from pmdarima.model_selection import train_test_split그 후 Pandas DataFrame 타입의 인풋 데이터를 준비한다. 아래와 같이 datetime 타입의 'date' 라는 열과 float 타입의 'death_rate'라는 열을 만들었다. 이 인풋데이터를 forecast_data 라고 저장했다고 가정하자.

그 후, 이 데이터를 training 데이터와 validation 데이터로 나눈다.
training 데이터를 이용해서 모델을 훈련하고, validation 데이터를 이용해서 모델의 성능을 확인할 것이다.
2020년 12월 12일까지의 데이터를 이용해서 훈련, 12월 6일 이후의 값을 예측한 후, 실제 12월 6일 이후의 값과 비교해서 성능을 확인한다.
# train 데이터와 validation 데이터 나누기.
X_train = forecast_data[forecast_data['date'] < '2020-12-13']
X_valid = forecast_data[forecast_data['date'] >= '2020-12-06']
# 예측한 열만 필터링하기
nyc = X_train[['date', 'death_rate']]
nyc_v = X_valid[['date', 'death_rate']]
# 각 데이터의 사이즈 확인하기
print('X_train Shape', X_train.shape)
print('X_Valid Shape', X_valid.shape)시계열 데이터의 시간을 담당하는 부분은 꼭 datetime 타입으로 전환해서 사용해야 된다.
# Date 를 dataframe의 인덱스로 만들어주기
nyc.set_index('date', inplace=True)
nyc_v.set_index('date', inplace=True)
# 4주간의 값을 예측할 것이므로 예측날짜들을 인덱스로 한 dataframe 만들기
index_4_weeks = pd.date_range(nyc.index[-1], freq='W', periods = 4, tz = None)
# 확인해보기
index_4_weeks결과값:
DatetimeIndex(['2020-12-06', '2020-12-13', '2020-12-20', '2020-12-27'], dtype='datetime64[ns]', freq='W-SUN')
본격 모델 돌리기..
order= 뒤에 (p,d,q)의 값을 정해 넣어주면 된다.
# order 에 파라미터 넣어주기.
model_arima = ARIMA(nyc, order=(1,0,2))
model_arima_fit = model_arima.fit(disp=-1)
# 예측한 값들을 저장
fcast1 = model_arima_fit.forecast(4)[0]
fcast1 = pd.Series(fcast1, index=index_4_weeks)
fcast1 = fcast1.rename("Arima")
# 확인
fcast1결과값:
2020-12-06 0.774338
2020-12-13 0.930663
2020-12-20 1.069161
2020-12-27 1.000975
Freq: W-SUN, Name: Arima, dtype: float64
이제 예측된 값을 시각화해보자.
# 예측값 plot 하기
fig, ax = plt.subplots(figsize=(15,5))
chart = sns.lineplot(x='date', y='death', data = nyc)
chart.set_title('New York-Newark-Jersey City COVID-19 Induced Death')
fcast1.plot(ax=ax, color='red', marker="o", legend=True)
nyc_v.plot(ax=ax, color='blue', marker="o", legend=True)
# AIC 프린트하기
print('The MSE of ARIMA is:', mean_squared_error(nyc_v['death'].values, fcast1.values, squared=False))결과값:
The MSE of ARIMA is: 0.09129622751300906
최적의 (p,d,q)값을 찾기 위해선 어떻게 해야할까?
우선 첫번째 방법은 가능한 모든 (p,d,q)값을 돌려보고 가장 높은 정확도를 주는 쌍을 고르는 것이다. for문을 통해서 p,d,q 가 각각 0부터 4까지의 값일 때 AIC (Akaike information criterion) 가 얼마정도 되는지 프린트 한다. 프린트된 결과를 보고, 가장 낮은 값을 가진 p,d,q 쌍을 고르면 된다.
import itertools
p=d=q=range(0,5)
pdq = list(itertools.product(p,d,q))
for param in pdq:
try:
model_arima = ARIMA(chicago,order=param)
model_arima_fit = model_arima.fit()
print(param,model_arima_fit.aic)
except:
continue
결과값 예시:
이 예시에서는 (1,0,4) 쌍이 제일 AIC가 낮다.

4. Auto-ARIMA 모델
두번째는 Auto-ARIMA 모델을 이용하는 것이다. 앞에서는 직접 iteration을 돌려보고 최적의 p,d,q 값을 정해야했지만, Auto-ARIMA 모델을 이용하면 모델이 알아서 최적의 값을 정해준다. 하지만 결과를 보면 알 수 있듯이, 직접 최적 값을 찾을 때와 값이 다른 것을 알 수 있다. Auto-ARIMA 모델은 AIC 만 보는 것이 아니라 복합적인 척도가 있기 때문이라고 한다.
# Auto-ARIMA 돌리기 - 계측값이 일별이면 m=1, 월별이면 m=12, 주별이면 m=52,
# 계절성이 있는 데이터면 seasonal=True 로 바꿔야함. 알아서 d 값을 찾아줌.
auto_arima_model = pm.auto_arima(nyc, seasonal=False, m=52)
# 모델 예측
fcast2 = auto_arima_model.predict(4)
fcast2 = pd.Series(fcast2, index=index_4_weeks)
fcast2 = fcast2.rename("Auto Arima")
# 예측값 시각화
fig, ax = plt.subplots(figsize=(15,5))
chart = sns.lineplot(x='date', y='death', data = nyc)
chart.set_title('New York-Newark-Jersey City')
fcast2.plot(ax=ax, color='red', marker="o", legend=True)
nyc_v.plot(ax=ax, color='blue', marker="o", legend=True)
# AIC 프린트하기
print('The MSE of auto-arima is:', mean_squared_error(nyc_v['death'].values, fcast2.values, squared=False))결과값:
The MSE of auto-arima is: 0.5152136019417364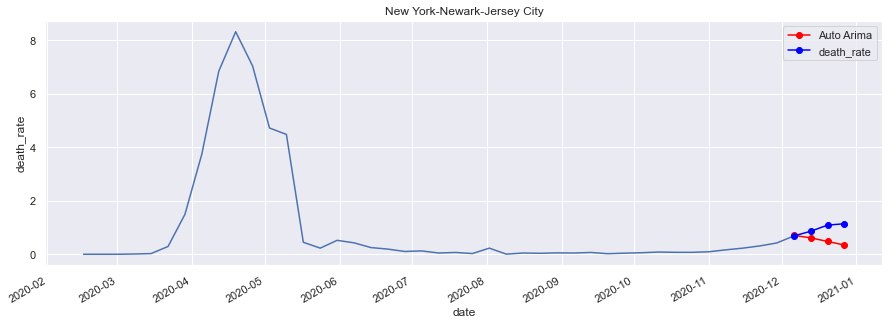
짜잔.
아리마에 대한 공부는 유튜브를 통해 제일 많이했다.
여기서 가장 많이 참고한 영상은 요것이다.
Reference: https://www.youtube.com/watch?v=axjgEgBgIY0

다음에 기회가 되면 Vector AR 모델 (VAR), 페이스북에서 만든 Facebook Prophet 모델을 알아보겠다.



